[문제1] 한 학생이 3학년 2학기 중간고사 답안지를 채점한 결과, 과목별 점수가 70, 90, 100, 45, 90이었다면 이 학생의 평균 점수는 얼마인가?
[문제2] 우리 서비스는 8월 300만 MAU를 보유하고 있었다. 9월에는 10%가 증가하였고, 10월에는 50%, 11월에는 다시 60%가 감소하였다. 3개월간 평균 MAU 증가율은 얼마인가?
평균을 모르는 사람은 아무도 없습니다. 초등학교 때 처음 산술 평균을 배우고, 고학년으로 진학하면 심화한 가중 평균이나 기하평균 등을 배우는데요, 사실 사람들이 평균을 종류별로 구분하여 적재적소 올바르게 활용하는 것은 아닙니다.
대다수 데이터 분석 툴에서 산술평균 외에는 제공하지 않는 추세이고, 실무자 또한 많은 수치들을 산술평균으로 계산하곤 합니다.
하지만 을 가지는 녀석입니다. 데이터 해석의 왜곡을 일으키지 않기 위해서는 다양한 평균의 개념을 알아두고, 용도에 맞게 해석해야 합니다.
오늘 뷰저블이 소개하는 데이터 분석 인사이트 내용은 ‘통계의 기본이라 불리우는 대표 값과 평균’입니다.
대표 값 3가지, 최빈값과 중앙값 그리고 평균
평균을 이해하기 전, 꼭 알아야 할 개념이 있습니다. 바로입니다. 대표 값이란, 말 그대로 데이터를 설명하기 위한 대표적인 값을 의미하는데요, 수천수만 가지의 데이터가 있더라도 실무자는 그 데이터를 다 살펴볼 시간이 없습니다.
결국은 액션(Action)에 중요한 대표 데이터가 무엇인지를 갖고 의사결정을 내리기 때문에 무엇을 대표 값으로 볼 것인지 적절히 판단해야 하며 우리에게 데이터가 주어졌을 때, 과연 적절한 수치인지 분별할 수 있어야 합니다. 가장 자주 쓰이는 대표 값으로는 ‘평균’과 ‘중앙값’, ‘최빈값’이 있고, 각각 아래 의미를 나타냅니다.
1. 최빈값(Mode)
표본에서 ‘가장 자주 발생한 값’을 의미합니다. 지지하는 정당이나 좋아하는 색처럼 ‘수’가 없거나, 혹은 수가 있더라도 대소관계가 의미 없는 자료에서 많이 사용됩니다. (예: 학생들의 키를 5센티미터 단위로 나눠 가장 많은 학생이 속한 범위)
2. 중앙값(Median)
표본에서 중앙에 위치하는 값 또는 그 이하가 표본의 절반을 차지하는 값을 의미합니다. 소득, 성적처럼 우열을 가릴 수 있는 ‘순위’가 중요한 자료에서 많이 쓰입니다. (예: 학생을 키 순서대로 세웠을 때 21명의 학생 중 11번째로 높은 학생의 키)
3. 평균(Mean)
여기서 말하는 평균은 ‘산술 평균’을 의미합니다. 표본을 모두 더한 후 해당 표본의 수로 나눈 값으로 사람들이 가장 즐겨 쓰는 대표 값으로, 다양한 애널리틱스에서 제공하는 체류 시간도 이렇게 구한 값이죠.
하지만 소득이나 체류 시간 등을 평균으로 구했을 때 불균형 즉, 편차가 커지면 커질수록 평균은 의미를 잃기 때문에 위에서 말한 중앙값과 구분해낼 분별력이 필요합니다. (예: 전체 학생의 키를 다 더한 값을 인원수로 나눴을 때)
그럼 위 개념들이 그래프상으로 어디쯤 위치하는지를 살펴보겠습니다. 빨간색은 최빈값, 파란색은 중앙값, 초록색이 (산술)평균입니다.
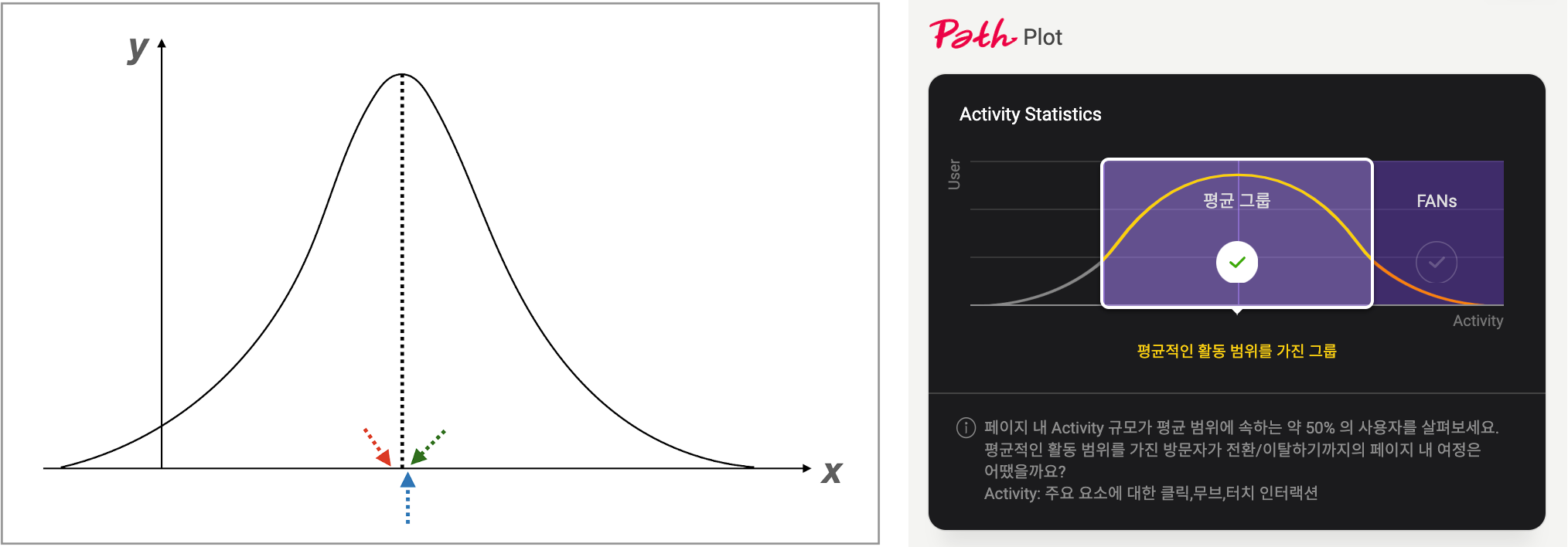
이전 정규분포 글에서 본 적 있는 종형 그래프입니다. 이렇게 그래프의 봉우리가 단봉이면서도 좌우 대칭을 이루면 최빈값과 중앙값, 평균이 모두 같습니다.
보통 많은 사람이 ‘평균’을 생각했을 때 이런 정규분포를 따른다고 생각해서, 전교 300명 중 본인이 150등 하면 ‘평균’ 정도는 되겠다고 생각하곤 하지만, 진실이 아닐 수도 있습니다.
뷰저블의 Path Plot 기능에서도 여러분의 쉬운 이해를 돕기 위해 정규분포 그래프를 채용했지만, 실제 사용자들의 움직임은 사이트마다 전혀 다른 모양으로 나타날 수 있습니다. 다른 분포 모양 그래프들도 살펴볼까요?
함께 보면 좋은 글 평균 고객의 행동을 나타내는 정규분포 이해하기
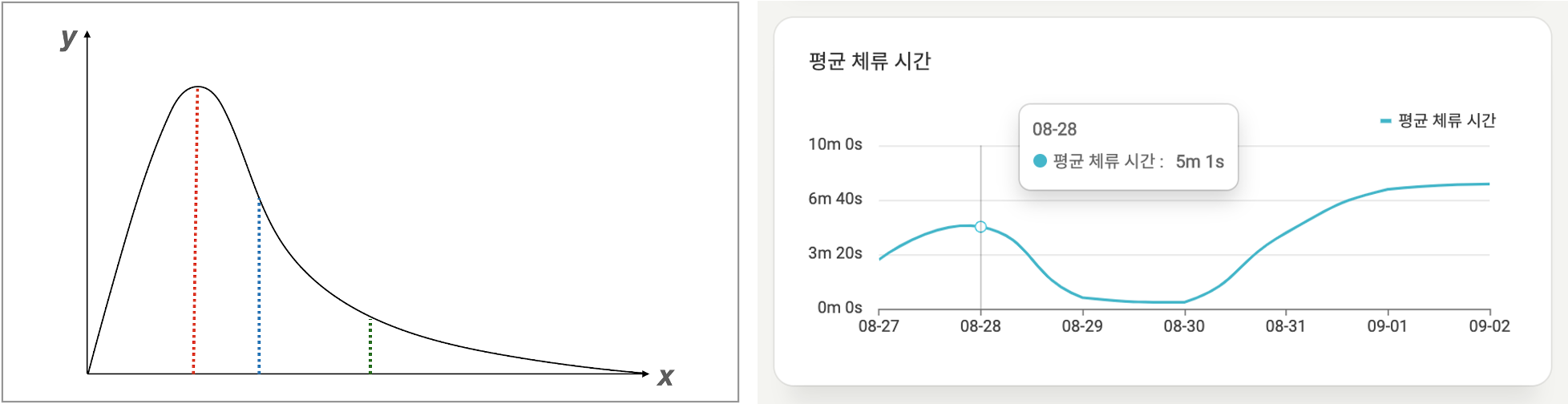
위처럼 단봉이지만 오른쪽으로 꼬리가 긴 롱테일 형은 지수분포나 카이제곱분포가 해당하는데요, 최빈값 ≤ 중앙값 ≤ 평균값을 따릅니다.
뷰저블이나 구글 애널리틱스에서 특정 페이지의 평균 체류 시간이 5분이더라도, 최빈값이 2분이라면 해당 사이트는 보편적으로 사람들이 2분 내에서 활동한다고 해석할 수 있습니다. 또, 특정 버튼을 고객이 평균 10회 클릭하더라도 최빈값은 3회~4회일 수 있습니다.
최빈값과 산술평균을 올바르게 분별하여 해석하면, 사용자의 행동 데이터를 이해하는 데 큰 도움이 됩니다.
함께 보면 좋은 글 카이제곱 분포
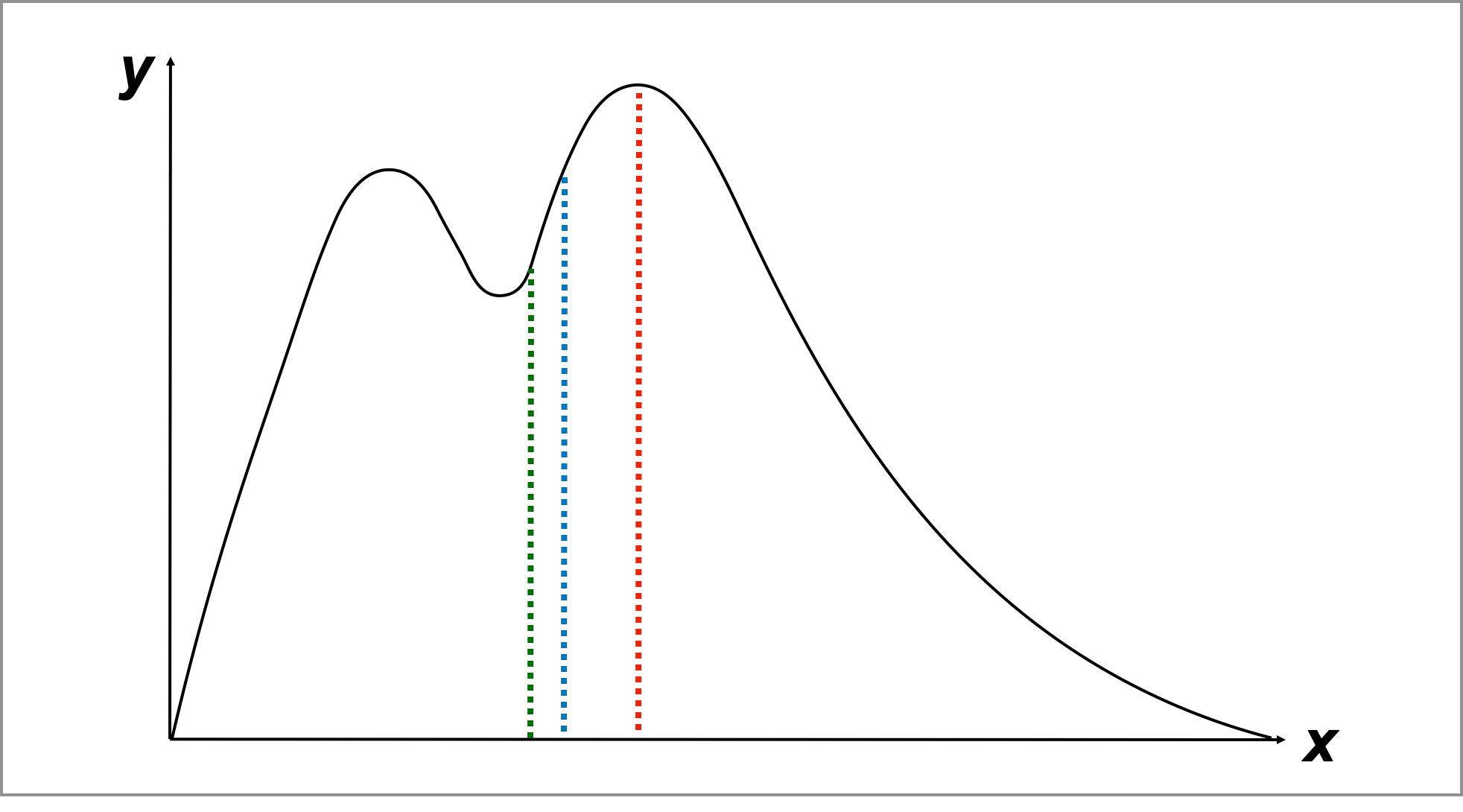
낙타 등처럼 봉우리가 2개 이상일 경우에는 어떨까요?
중앙값과 평균값에 일관성이 없고, 최빈값은 가장 고지대 산봉우리에서 형성됩니다. 예를 들어 수능시험을 본다면 최선을 다해 열심히 하는 사람이 있는가 하면 아예 놀아버리는 사람도 있을 것입니다. 그럼 중앙값과 평균에 일관성이 없고 최빈값은 가장 높은 극대점에서 형성됩니다.
평균의 기본, 산술평균과 기하평균 그리고 조화평균
대표 값에서 설명한 평균은 산술평균인데요, 이 외에도 자주 쓰이는 평균으로는 기하평균과 조화평균이 있습니다.
기하평균은 엑셀로 ‘GEOMENA()’, 조화평균은 ‘HARMEAN()’으로 구할 수 있습니다. 산술평균은 위에서도 말한 것처럼 가장 일반적인 평균으로 모든 데이터의 합을 데이터의 수로 나눈 값입니다. 그럼 기하평균과 조화평균은 무엇일까요?
물가 상승률 등의 비율 평균을 구할 때 활용되는 기하평균
입니다. 일반적으로 ‘상승률’이나 ‘하락률’을 활용한 계산에 쓰이는데요!
식당에서 김치찌개의 가격을 정할 때 어떻게 응용할 수 있을지를 예로 소개해 드리겠습니다.
여러분들은 어떤 메뉴를 고르실 건가요? 오랜만에 거금이지만 몸보신을 하고 싶은 사람이라면 전복해물 김치찌개를 선택할 것이고, 매일 밖에서 밥을 사먹는 평범한 직장인이라면 점심시간 참치 김치찌개만으로도 가격이 꽤 나간다고 생각할 것입니다.
위 메뉴판은 제가 임의로 설정한 가격인데요, 참치가 10,000원, 전복해물이 30,000원입니다.
이 때 가운데에 적힌 우삼겹 김치찌개의 가격설정을 산술평균으로 구했더니 20,000원, 기하평균으로 계산하면 17,300원이 계산되었는데요, 여러분들이라면 얼마로 설정하시겠습니까?
다시 원조아구찜 메뉴판을 임의로 가져왔습니다. 메뉴의 사이즈가 올라갈수록 가격 또한 함께 올라가는데요, 기본과 대 사이즈 메뉴를 기하평균으로 계산하였더니 37,230원이 나왔고 단순 산술평균으로 계산하였더니 37,500원이 나왔습니다.
실제 가격과 기하평균으로 산정한 가격이 더 맞죠? 이처럼 가 나옵니다.
한 가지 더 예를 들어보겠습니다. 1,000원짜리 주식이 10% 상승한 후 다시 10% 하락하였다면, 여러분들은 가격변동이 없다고 생각할지 모릅니다.
하지만 실제 그랬을까요? 1,000원이 10% 상승하면 1,100원이 됩니다. 헌데 다시 10% 하락하면 1,100원이 990원이 되어 10원 손해를 보았죠. 수식으로 표현하면 (1.1 X 0.9)^0.5=0.00 즉, 천원의 0.99원은 990원이 됩니다.
MAU가 지난달 10% 상승해서 이번 달 다시 10% 하락하였다면, 마찬가지로 MAU가 원상복구 된 것이 아닌, 하락한 것이라고 이해할 수 있습니다. 이해하셨나요?
평균적인 변화율을 구할 때는, 조화평균
운동장을 두 바퀴 돌았을 때의 평균 속력을 어떻게 구할까요? 1Km 코스를 한 바퀴 돌 때는 시간당 10Km 속력으로, 두 바퀴째 돌 때는 시간당 8Km 속력으로 구했을 때의 평균을 구하면, 단순히 산술평균으로는 (10+8)2=9Km/h가 됩니다.
하지만 실제로도 그럴까요? 한 바퀴 돌 때 1/10=0.1시간, 두 바퀴 돌 때 1/8=0.125시간이 들어 총 0.225시간이 걸렸기 때문에 (1+1)/0.225=8.89Km/h가 정확한 수식이 됩니다.
이처럼, 됩니다.
오늘은 데이터 분석을 할 때 수치 해석에 가장 중요한 기본 중의 기본, 대표값과 평균에 대해 알아보았습니다.
산술평균으로만을 다양한 데이터들을 해석하고 활용하시고 계셨다면, 더 정확한 자료 분석을 위해 애널리틱스의 결과값을 다른 평균으로는 구할 수 없을지, 최빈값으로 보는 것이 맞을지 등을 확인해보세요!
